dhkwak-Introduction of Deep Reinforcement Learning.html
https://www.youtube.com/watch?v=dw0sHzE1oAc&t=378s
Reinforcement learning:
Goal is to find policy function p(a|s) which maximizes sum of reward
s: current state where agent which you train is in
a: in that state, what action agent should do?
================================================================================
When you want to find policy,
you need cycle composed of "agent", "environment", "interaction"(state, reward, action) as tool
 To define above cycle, you need mathematical tool called MDP (Markov Decision Processes)
You will inspect MDP in 3 steps
(Markov Process, Markov Reward Process, Markov Decision Process)
================================================================================
Markov Process is defined by two factors
1. Discrete state space (like circles)
Suppose 5 by 5 maze
Mice can be located in 25 locations
In this case, size of state space is 25
1. State transition probability:
This is process of finding rule from environment
This is dynamics about environment
To define above cycle, you need mathematical tool called MDP (Markov Decision Processes)
You will inspect MDP in 3 steps
(Markov Process, Markov Reward Process, Markov Decision Process)
================================================================================
Markov Process is defined by two factors
1. Discrete state space (like circles)
Suppose 5 by 5 maze
Mice can be located in 25 locations
In this case, size of state space is 25
1. State transition probability:
This is process of finding rule from environment
This is dynamics about environment
 ================================================================================
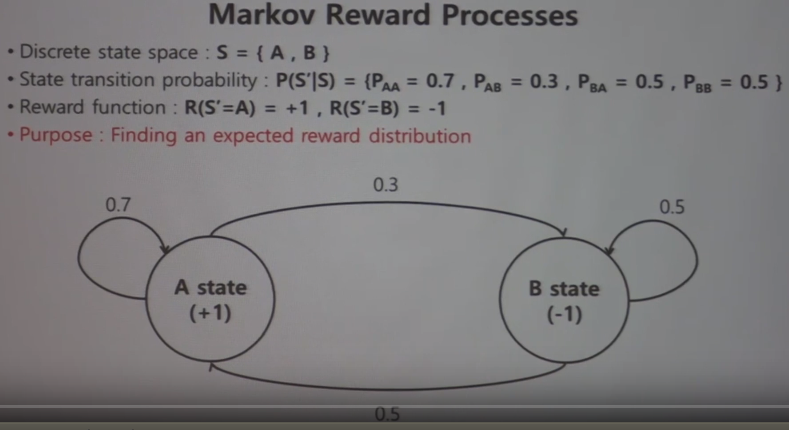
Markov Reward Process
This is concept which is added by "reward" (+1, -1) on "Markov Process"
So, you can let agent to know reward
If agent arrives to A state, agent will get +1 reward
MRP lets agent to know state A is better state and moving to A state is better action
================================================================================
Markov Reward Process
This is concept which is added by "reward" (+1, -1) on "Markov Process"
So, you can let agent to know reward
If agent arrives to A state, agent will get +1 reward
MRP lets agent to know state A is better state and moving to A state is better action
 ================================================================================
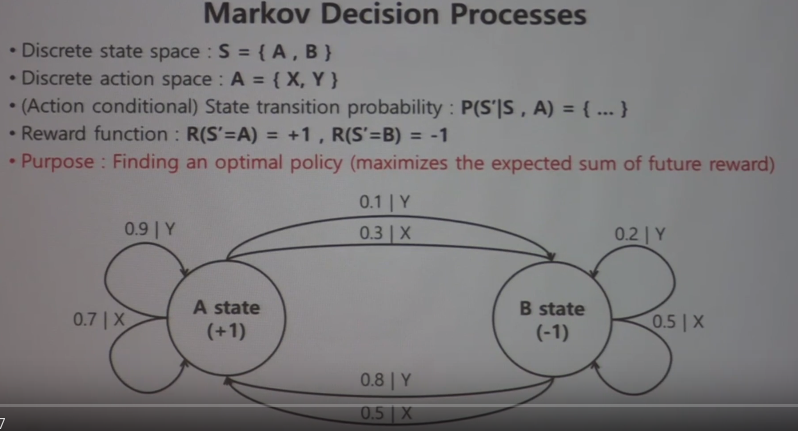
Markov Decision Process
This is added by "action" (X and Y) on MRP
In this example,
Discrete state space is S={A,B}
Discrete action space is A={X,Y}
(Action conditional) State transition probability:
$$$P(S'|S,A)={...}$$$
When you input state S and action A, what next state S' will be?
Reward function:
$$$R(S'=A)=+1, R(S'=B)=-1$$$
At state of A, which action will give agent more reward?
Finding policy for it is goal of reinforcement learning
At state A, agent has 2 options (action X, action Y)
Since moving to A gives + reward, it's true that moving to B is false action
So, if agent is in A, agent should stay in A
So, at state of A, optimal decision is to select action Y
By same logic, at state of B,
agent should make decision (Y in this case) to move to state of A
================================================================================
Markov Decision Process
This is added by "action" (X and Y) on MRP
In this example,
Discrete state space is S={A,B}
Discrete action space is A={X,Y}
(Action conditional) State transition probability:
$$$P(S'|S,A)={...}$$$
When you input state S and action A, what next state S' will be?
Reward function:
$$$R(S'=A)=+1, R(S'=B)=-1$$$
At state of A, which action will give agent more reward?
Finding policy for it is goal of reinforcement learning
At state A, agent has 2 options (action X, action Y)
Since moving to A gives + reward, it's true that moving to B is false action
So, if agent is in A, agent should stay in A
So, at state of A, optimal decision is to select action Y
By same logic, at state of B,
agent should make decision (Y in this case) to move to state of A
 ================================================================================
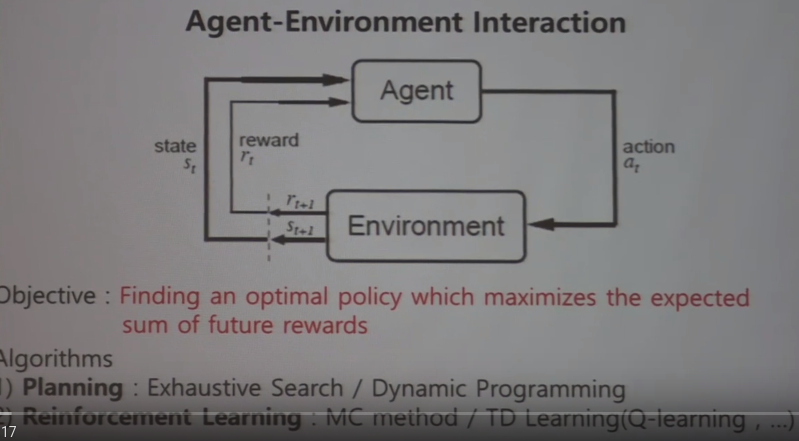
Summary: MDP is mathematical framework for modeling decision making
================================================================================
MDP question can be solved by two methods (planning, reinforcement learning)
Planning: Exhaustive search/Dynamic programming
Reinforcement Learning: Monte Carlo method/Temporal Difference learning(Q learning)
Dynamic programming is not machine learning methodology,
but similar to reinforcement learning in terms of mathematical way.
================================================================================
Summary: MDP is mathematical framework for modeling decision making
================================================================================
MDP question can be solved by two methods (planning, reinforcement learning)
Planning: Exhaustive search/Dynamic programming
Reinforcement Learning: Monte Carlo method/Temporal Difference learning(Q learning)
Dynamic programming is not machine learning methodology,
but similar to reinforcement learning in terms of mathematical way.
 Above agent considers entire summed reward up to all future cases,
which means agent can eat -1 reward to get +3 reward which is + summed reward in the end.
Reinforcement learning wants to deal with "sparse reward" problem and "delayed reward" problem
================================================================================
You have 2 methodologies (Planning, Reinforcement Learning) to find expectation value
- Planning:
You already know probability of each side occurring
from trial rollowing dice as $$$\frac{1}{6}$$$ for one event
In this case, you can find expection value (3.5) easily.
$$$1 \times \dfrac{1}{6}+2 \times \dfrac{1}{6}+...+6 \times \dfrac{1}{6}=3.5$$$
- Reinforcement Learning:
When you don't know probability of each side occurring,
you should find expectation value by performing manual trials
You should roll dice like 100 times, then you find mean value of occurred dice side
================================================================================
You should consider "discount factor" to complete Markov Decision Process model
Discount factor is concept which was created to mathematically define "future reward"
Sum of future rewards $$$G_{t}$$$ in "episodic tasks"
$$$G_{t}=R_{t+1}+R_{t+2}+...+R_{T}$$$
Episodic task: task which has end point (T), for example, GO match
t: arbitary current time point
R: reward
Continuous tasks: task which has no end point (T), for example, car driving, stock market
Sum of "future rewards" $$$G_{t}$$$ in continuous tasks
$$$G_{t}=R_{t+1}+R_{t+2}+...+R_{T}+...$$$
$$$G_{t}$$$ can be diverged
$$$G_{t} \rightarrow \infty$$$
To mathematically manage above cases,
you multiply "discount factor" ($$$0<= \gamma<1$$$)
Sum of "discounted future rewards" in both case
$$$G_{t}:=R_{t+1}+\gamma R_{t+2}+\gamma^{2}R_{t+3}+...+\gamma^{T-1}R_{T}+...$$$
$$$G_{t}:= \sum\limits_{k=1}^{\infty} \gamma^{k-1}R_{t+k} $$$ (This will be converged)
There are 2 kinds of policy (deterministic policy, stochastic policy),
And policy is target of train
And policy is function that lets agent to know what action he should do
Above agent considers entire summed reward up to all future cases,
which means agent can eat -1 reward to get +3 reward which is + summed reward in the end.
Reinforcement learning wants to deal with "sparse reward" problem and "delayed reward" problem
================================================================================
You have 2 methodologies (Planning, Reinforcement Learning) to find expectation value
- Planning:
You already know probability of each side occurring
from trial rollowing dice as $$$\frac{1}{6}$$$ for one event
In this case, you can find expection value (3.5) easily.
$$$1 \times \dfrac{1}{6}+2 \times \dfrac{1}{6}+...+6 \times \dfrac{1}{6}=3.5$$$
- Reinforcement Learning:
When you don't know probability of each side occurring,
you should find expectation value by performing manual trials
You should roll dice like 100 times, then you find mean value of occurred dice side
================================================================================
You should consider "discount factor" to complete Markov Decision Process model
Discount factor is concept which was created to mathematically define "future reward"
Sum of future rewards $$$G_{t}$$$ in "episodic tasks"
$$$G_{t}=R_{t+1}+R_{t+2}+...+R_{T}$$$
Episodic task: task which has end point (T), for example, GO match
t: arbitary current time point
R: reward
Continuous tasks: task which has no end point (T), for example, car driving, stock market
Sum of "future rewards" $$$G_{t}$$$ in continuous tasks
$$$G_{t}=R_{t+1}+R_{t+2}+...+R_{T}+...$$$
$$$G_{t}$$$ can be diverged
$$$G_{t} \rightarrow \infty$$$
To mathematically manage above cases,
you multiply "discount factor" ($$$0<= \gamma<1$$$)
Sum of "discounted future rewards" in both case
$$$G_{t}:=R_{t+1}+\gamma R_{t+2}+\gamma^{2}R_{t+3}+...+\gamma^{T-1}R_{T}+...$$$
$$$G_{t}:= \sum\limits_{k=1}^{\infty} \gamma^{k-1}R_{t+k} $$$ (This will be converged)
There are 2 kinds of policy (deterministic policy, stochastic policy),
And policy is target of train
And policy is function that lets agent to know what action he should do
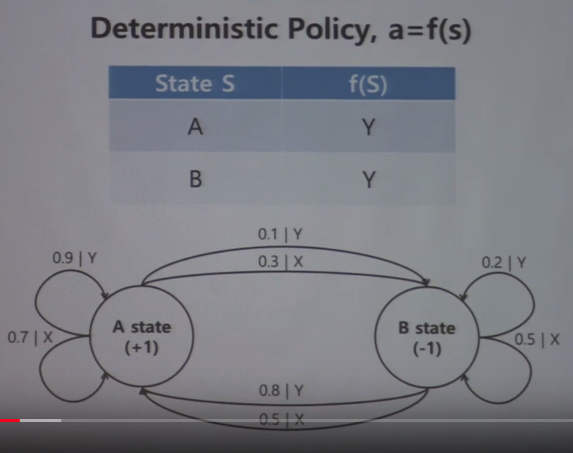
 Some cases are fitted to stochastic policy,
and some other cases are fitted to deterministic policy
================================================================================
You will see value-based-reinforment learning
Value is expection value of sum of future rewards, $$$E[G_{t}]$$$
You can write sum of future rewards in episodic tasks as following:
$$$G_{t}:=R_{t+1}+R_{t+2}+...+R_{T}$$$
You can write sum of future rewards in continuous tasks as following:
$$$G_{t}:=R_{t+1}+R_{t+2}+...+R_{T}+...$$$
$$$G_{t}\rightarrow \infty$$$ ($$$G_{t}$$$ diverges)
You can write sum of discounted future rewards in both cases
(episodic and continuous) as following
$$$G_{t}:=R_{t+1}+\gamma R_{t+2}+\gamma^{2}R_{t+3}+...+\gamma^{T-1}R_{T}+...$$$
$$$G_{t}:=\sum\limits_{k=1}^{\infty}\gamma^{k-1}R_{t+k}$$$
This version of $$$G_{t}$$$ converges
If you know value with respect to specific environment,
then, if you go along the way which gives most value,
then, you can maximize all reward up to the future reward
With above mechanism, when you decide policy, you can decide policy based on the value
Above way is value based reinforcement learning.
================================================================================
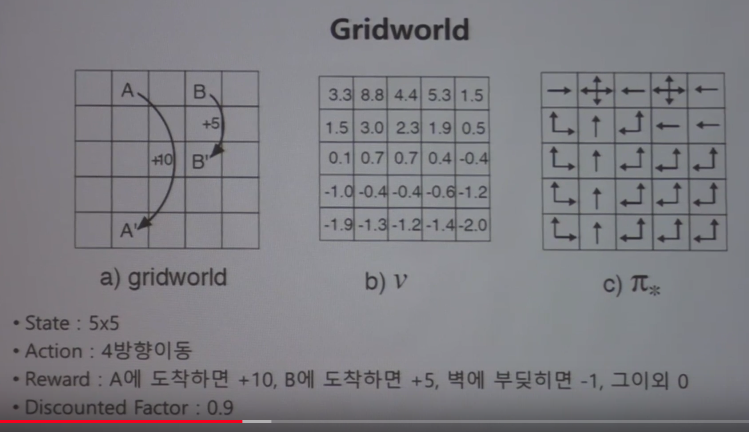
b) is values at each state
c) is optimal policy at each state
Number of state of this question is 25 $$$(5\times5)$$$
Number of action of this question is 4 (up, down, left, right)
Reward of this question is +10 if you arrive to A' from A
Reward of this question is +5 if you arrive to B' from B
Reward of this question is -1 if you bump the wall
Reward of this question is 0 if other cases occur
Discount factor of this question is 0.9
Some cases are fitted to stochastic policy,
and some other cases are fitted to deterministic policy
================================================================================
You will see value-based-reinforment learning
Value is expection value of sum of future rewards, $$$E[G_{t}]$$$
You can write sum of future rewards in episodic tasks as following:
$$$G_{t}:=R_{t+1}+R_{t+2}+...+R_{T}$$$
You can write sum of future rewards in continuous tasks as following:
$$$G_{t}:=R_{t+1}+R_{t+2}+...+R_{T}+...$$$
$$$G_{t}\rightarrow \infty$$$ ($$$G_{t}$$$ diverges)
You can write sum of discounted future rewards in both cases
(episodic and continuous) as following
$$$G_{t}:=R_{t+1}+\gamma R_{t+2}+\gamma^{2}R_{t+3}+...+\gamma^{T-1}R_{T}+...$$$
$$$G_{t}:=\sum\limits_{k=1}^{\infty}\gamma^{k-1}R_{t+k}$$$
This version of $$$G_{t}$$$ converges
If you know value with respect to specific environment,
then, if you go along the way which gives most value,
then, you can maximize all reward up to the future reward
With above mechanism, when you decide policy, you can decide policy based on the value
Above way is value based reinforcement learning.
================================================================================
b) is values at each state
c) is optimal policy at each state
Number of state of this question is 25 $$$(5\times5)$$$
Number of action of this question is 4 (up, down, left, right)
Reward of this question is +10 if you arrive to A' from A
Reward of this question is +5 if you arrive to B' from B
Reward of this question is -1 if you bump the wall
Reward of this question is 0 if other cases occur
Discount factor of this question is 0.9
 ================================================================================
When you proceed value-based-reinforcement learning,
you first need to find all values at each state
But from now on, you will approximate value into value function
"Value function" lets you to know expected sum of future rewards, at given state s,
when following policy $$$\pi$$$
Value function takes in the state as the input, and value function outputs the value
1. State-value function
$$$v_{\pi}(s)\doteq E_{\pi}[G_{t}|S_{t}=s]$$$
$$$v_{\pi}(s)\doteq E_{\pi}[\sum\limits_{k=0}^{\infty}\gamma^{k}R_{t+k+1}|S_{t}=s]$$$
If you use only state-value function,
to make decision for action,
you should need to explore values around state you're being in
You should simulate all candidate actions you can choose,
to inspect next state's values
This method is called "one step ahead search" for all actions
So, when you find policy from state value function,
you always need to explore values what next state gives
In real world situation, one step ahead search is almost not possible to use,
for example, think of autonomous car.
================================================================================
To resolve above issue, you should build "model environment" reflecting real environment
Then you should find all values in advance
This methodology is called "model-based-reinforcement learning",
where you first fully train RL network in virtual environment
================================================================================
Or, you can use (state)-action-value function to resolve above issue
1. (State)-Action-value function
$$$q_{\pi}(s,a) \doteq E_{\pi}[S_{t}-s,A_{t}=a]$$$
$$$v_{\pi}(s) \doteq E_{\pi}[\sum\limits_{k=0}^{\infty}\gamma^{k}R_{t+k+1}|S_{t}=s,A_{t}=a$$$
This way doesn't require one step ahead search
because finding values at next stats are already calculated in advance
You can find value when you do action a at state s
Note that you input state s and action a into q function,
unlike state value function takes in state s as input
================================================================================
Policy from action value function
$$$a=f(s)=arg_{a}max\;{q_{\pi}(s,a)}$$$
Suppose you have 4 candidate actions.
Then you can try to input 4 actions one by one
You will obtains 4 outputs from action value function
Then, you can choose argument a which creates highest output
================================================================================
When you proceed value-based-reinforcement learning,
you first need to find all values at each state
But from now on, you will approximate value into value function
"Value function" lets you to know expected sum of future rewards, at given state s,
when following policy $$$\pi$$$
Value function takes in the state as the input, and value function outputs the value
1. State-value function
$$$v_{\pi}(s)\doteq E_{\pi}[G_{t}|S_{t}=s]$$$
$$$v_{\pi}(s)\doteq E_{\pi}[\sum\limits_{k=0}^{\infty}\gamma^{k}R_{t+k+1}|S_{t}=s]$$$
If you use only state-value function,
to make decision for action,
you should need to explore values around state you're being in
You should simulate all candidate actions you can choose,
to inspect next state's values
This method is called "one step ahead search" for all actions
So, when you find policy from state value function,
you always need to explore values what next state gives
In real world situation, one step ahead search is almost not possible to use,
for example, think of autonomous car.
================================================================================
To resolve above issue, you should build "model environment" reflecting real environment
Then you should find all values in advance
This methodology is called "model-based-reinforcement learning",
where you first fully train RL network in virtual environment
================================================================================
Or, you can use (state)-action-value function to resolve above issue
1. (State)-Action-value function
$$$q_{\pi}(s,a) \doteq E_{\pi}[S_{t}-s,A_{t}=a]$$$
$$$v_{\pi}(s) \doteq E_{\pi}[\sum\limits_{k=0}^{\infty}\gamma^{k}R_{t+k+1}|S_{t}=s,A_{t}=a$$$
This way doesn't require one step ahead search
because finding values at next stats are already calculated in advance
You can find value when you do action a at state s
Note that you input state s and action a into q function,
unlike state value function takes in state s as input
================================================================================
Policy from action value function
$$$a=f(s)=arg_{a}max\;{q_{\pi}(s,a)}$$$
Suppose you have 4 candidate actions.
Then you can try to input 4 actions one by one
You will obtains 4 outputs from action value function
Then, you can choose argument a which creates highest output
 ================================================================================
Job which following 2 algorithms (planning, RL) want to do is
to find value table or value function you saw
As you saw, formulars of state value function and action value function contain expectation
- State value function
$$$v_{\pi}(s)\doteq E_{\pi}[G_{t}|S_{t}=s]$$$
$$$v_{\pi}(s)\doteq E_{\pi}[\sum\limits_{k=0}^{\infty}\gamma^{k}R_{t+k+1}|S_{t}=s]$$$
- (State)-Action-value function
$$$q_{\pi}(s,a) \doteq E_{\pi}[S_{t}-s,A_{t}=a]$$$
$$$v_{\pi}(s) \doteq E_{\pi}[\sum\limits_{k=0}^{\infty}\gamma^{k}R_{t+k+1}|S_{t}=s,A_{t}=a$$$
When you find expection value,
if you find expectation value with knowing probability, it's planning,
if you find expectation value without knowing probability but experience,
it's machine/deep/reinforment learing
================================================================================
Job which following 2 algorithms (planning, RL) want to do is
to find value table or value function you saw
As you saw, formulars of state value function and action value function contain expectation
- State value function
$$$v_{\pi}(s)\doteq E_{\pi}[G_{t}|S_{t}=s]$$$
$$$v_{\pi}(s)\doteq E_{\pi}[\sum\limits_{k=0}^{\infty}\gamma^{k}R_{t+k+1}|S_{t}=s]$$$
- (State)-Action-value function
$$$q_{\pi}(s,a) \doteq E_{\pi}[S_{t}-s,A_{t}=a]$$$
$$$v_{\pi}(s) \doteq E_{\pi}[\sum\limits_{k=0}^{\infty}\gamma^{k}R_{t+k+1}|S_{t}=s,A_{t}=a$$$
When you find expection value,
if you find expectation value with knowing probability, it's planning,
if you find expectation value without knowing probability but experience,
it's machine/deep/reinforment learing
 ================================================================================
One of solutions for MDP: Planning
You should have precondition to perform planning
You should know state transition probability that is you should perform simulation
Planning has 2 algorithms (exhaustive search, dynamic programming)
================================================================================
One of solutions for MDP: Planning
You should have precondition to perform planning
You should know state transition probability that is you should perform simulation
Planning has 2 algorithms (exhaustive search, dynamic programming)
 ================================================================================
N: number of state
================================================================================
N: number of state
 ================================================================================
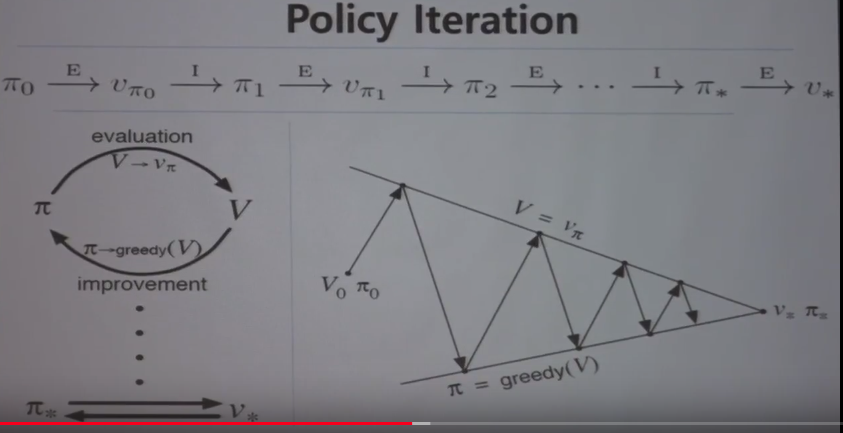
Policy iteration algorithm uses dynamic programming algorithm from planning
Policy iteration consists of 2 steps (policy evaluation and policy improvement)
================================================================================
Policy iteration algorithm uses dynamic programming algorithm from planning
Policy iteration consists of 2 steps (policy evaluation and policy improvement)

 ================================================================================
- Policy evaluation:
By using knowledge you know, you make current value function more precise.
$$$v_{\pi}(s)\doteq E_{\pi}[R_{t+1}+\gamma R_{t+2}+\gamma^{2}R_{t+3}+...|S_{t}=s]$$$
$$$v_{\pi}(s)\doteq E_{\pi}[R_{t+1}+\gamma v_{\pi}(S_{t+1})|S_{t}=s]$$$
$$$v_{\pi}(s)=\sum\limits_{a}\pi(a|s)\sum\limits_{s',r}p(s',r|s,a)[r+\gamma v_{\pi}(s')]$$$
Key formular to perform policy evaluation (which updates value function) is:
$$$v_{\pi}(s)\doteq E_{\pi}[R_{t+1}+\gamma v_{\pi}(S_{t+1})|S_{t}=s]$$$
- Policy improvement:
By using more precise value function, you try to make more optimal decision for more reward
$$$\pi'(s)\doteq arg_{a}max\;q_{\pi}(s,a)$$$
$$$\pi'(s)\doteq arg_{a}max\;E[R_{t+1}+\gamma v_{\pi}(S_{t+1})|S_{t}=s,A_{t}=a]$$$
$$$\pi'(s)\doteq arg_{a}max\;\sum\limits_{s',r}p(s',r|s,a)[r+\gamma v_{\pi}(s')]$$$
Key formular to perform policy improvement (which produces more reward) is:
$$$\pi'(s)\doteq arg_{a}max\;q_{\pi}(s,a)$$$
Then, finally you can find optimal value function and policy
================================================================================
To reduce number of cases, you can use dynamic programming
================================================================================
- Policy evaluation:
By using knowledge you know, you make current value function more precise.
$$$v_{\pi}(s)\doteq E_{\pi}[R_{t+1}+\gamma R_{t+2}+\gamma^{2}R_{t+3}+...|S_{t}=s]$$$
$$$v_{\pi}(s)\doteq E_{\pi}[R_{t+1}+\gamma v_{\pi}(S_{t+1})|S_{t}=s]$$$
$$$v_{\pi}(s)=\sum\limits_{a}\pi(a|s)\sum\limits_{s',r}p(s',r|s,a)[r+\gamma v_{\pi}(s')]$$$
Key formular to perform policy evaluation (which updates value function) is:
$$$v_{\pi}(s)\doteq E_{\pi}[R_{t+1}+\gamma v_{\pi}(S_{t+1})|S_{t}=s]$$$
- Policy improvement:
By using more precise value function, you try to make more optimal decision for more reward
$$$\pi'(s)\doteq arg_{a}max\;q_{\pi}(s,a)$$$
$$$\pi'(s)\doteq arg_{a}max\;E[R_{t+1}+\gamma v_{\pi}(S_{t+1})|S_{t}=s,A_{t}=a]$$$
$$$\pi'(s)\doteq arg_{a}max\;\sum\limits_{s',r}p(s',r|s,a)[r+\gamma v_{\pi}(s')]$$$
Key formular to perform policy improvement (which produces more reward) is:
$$$\pi'(s)\doteq arg_{a}max\;q_{\pi}(s,a)$$$
Then, finally you can find optimal value function and policy
================================================================================
To reduce number of cases, you can use dynamic programming
 ================================================================================
Temporal Difference Learning
This shows good performance
Good point of Monte Carlo is Monte Carlo can train your network from actual experience
Good point of dynamic programming is dynamic programming reduces quantity of calculation
because dynamic programming only calculates with respect to 2 timesteps
TD is combined algorithm from above 2 good points
================================================================================
Difference between SARSA and Q learning
Formulars are almost same.
- This is SARSA notation
$$$Q(s_{t},a_{t}) \leftarrow Q(s_{t},a_{t})+\alpha[r_{t+1}+\gamma Q(s_{t+1},a_{t+1})-Q(s_{t},a_{t})]$$$
$$$[r_{t+1}+\gamma Q(s_{t+1},a_{t+1}) - Q(s_{t},a_{t})]$$$ is loss of q function you're having now
You need 5 variables as input data ($$$s_{t}, a_{t}, r_{t+1}, s_{t+1}, a_{t+1}$$$) to create above notation
================================================================================
What's good point of SARSA algorithm?
If you use Monte Carlo method, you should proceed task up to end of episode,
then, you get values, then you apply obtained values to all states to update
If you use temporal difference learing,
you can update your network by using very next reward per every step
Both method can learn perfect value function with different methods
================================================================================
Q learning has "max" operator
SARSA is not good because it doesn't have "max" operator
$$$Q(s_{t},a_{t}) \leftarrow Q(s_{t},a_{t}) + \alpha [r_{t+1}+\gamma max_{a} Q(s_{t+1},a) - Q(s_{t},a_{t})]$$$
You need 4 variables as input data (s_{t}, a_{t}, r_{t+1}, s_{t+1}) to create above notation
Reason you need only 4 variables is because you use max operator with respect to general a
$$$ [r_{t+1}+\gamma max_{a} Q(s_{t+1},a) - Q(s_{t},a_{t})] $$$ is TD loss
You use size of TD loss as loss, then you train with regression way
$$$\text{Loss function L}=\frac{1}{2}[r+max_{a'}Q(s',a')-Q(s,a)]^{2}$$$
$$$r+max_{a'}Q(s',a')$$$ is target
Q(s,a) is prediction from model
================================================================================
Above difference between SARSA and q learning can also be notated
by difference between on policy and off policy
- on policy : SARSA is "on policy".
SARSA only can be used when target policy which you need to train is same
with behavior policy which you're using
- off policy:
It's fine with both cases either same or not same
Q learning is "off policy"
================================================================================
Unstationary target issue
================================================================================
Replay memory
================================================================================
Temporal Difference Learning
This shows good performance
Good point of Monte Carlo is Monte Carlo can train your network from actual experience
Good point of dynamic programming is dynamic programming reduces quantity of calculation
because dynamic programming only calculates with respect to 2 timesteps
TD is combined algorithm from above 2 good points
================================================================================
Difference between SARSA and Q learning
Formulars are almost same.
- This is SARSA notation
$$$Q(s_{t},a_{t}) \leftarrow Q(s_{t},a_{t})+\alpha[r_{t+1}+\gamma Q(s_{t+1},a_{t+1})-Q(s_{t},a_{t})]$$$
$$$[r_{t+1}+\gamma Q(s_{t+1},a_{t+1}) - Q(s_{t},a_{t})]$$$ is loss of q function you're having now
You need 5 variables as input data ($$$s_{t}, a_{t}, r_{t+1}, s_{t+1}, a_{t+1}$$$) to create above notation
================================================================================
What's good point of SARSA algorithm?
If you use Monte Carlo method, you should proceed task up to end of episode,
then, you get values, then you apply obtained values to all states to update
If you use temporal difference learing,
you can update your network by using very next reward per every step
Both method can learn perfect value function with different methods
================================================================================
Q learning has "max" operator
SARSA is not good because it doesn't have "max" operator
$$$Q(s_{t},a_{t}) \leftarrow Q(s_{t},a_{t}) + \alpha [r_{t+1}+\gamma max_{a} Q(s_{t+1},a) - Q(s_{t},a_{t})]$$$
You need 4 variables as input data (s_{t}, a_{t}, r_{t+1}, s_{t+1}) to create above notation
Reason you need only 4 variables is because you use max operator with respect to general a
$$$ [r_{t+1}+\gamma max_{a} Q(s_{t+1},a) - Q(s_{t},a_{t})] $$$ is TD loss
You use size of TD loss as loss, then you train with regression way
$$$\text{Loss function L}=\frac{1}{2}[r+max_{a'}Q(s',a')-Q(s,a)]^{2}$$$
$$$r+max_{a'}Q(s',a')$$$ is target
Q(s,a) is prediction from model
================================================================================
Above difference between SARSA and q learning can also be notated
by difference between on policy and off policy
- on policy : SARSA is "on policy".
SARSA only can be used when target policy which you need to train is same
with behavior policy which you're using
- off policy:
It's fine with both cases either same or not same
Q learning is "off policy"
================================================================================
Unstationary target issue
================================================================================
Replay memory















